Similarity invariance
In mathematics, similarity invariance is a property exhibited by a function whose value is unchanged under similarities of its domain. That is, 
is invariant under similarities if 
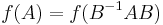where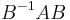 
is a similarity of A. Examples of such functions include the trace, determinant, and the minimal polynomial. A more colloquial phrase that means the same thing as similarity invariance is "basis independence."